Analisis Regresi Linier Berganda

Regresi linear adalah alat statistik yang dipergunakan untuk mengetahui pengaruh antara satu atau beberapa variabel terhadap satu buah variabel. Variabel yang mempengaruhi sering disebut variabel bebas, variabel independen atau variabel penjelas. Variabel yang dipengaruhi sering disebut dengan variabel terikat atau variabel dependen. Regresi linear hanya dapat digunakan pada skala interval dan rasio.

Analisis regresi linear merupakan metode statistik yang sering dipergunakan dalam penelitian-penelitian sosial, terutama penelitian ekonomi. Software yang paling banyak digunakan adalah SPSS.  

Secara umum regresi linear terdiri dari

a.      Regresi linear sederhana yaitu dengan satu variabel bebas (X) dan satu variabel terikat (Y)

b.      Regresi linear berganda dengan beberapa variabel bebas dan satu variabel terikat.

Penggunaan metode analisis regresi linear berganda memerlukan UJI ASUMSI KLASIK yang harus dipenuhi. Asumsi klasik yang sering digunakan adalah

a.      Asumsi Normalitas

b.      Asumsi Linearitas

c.       Heteroskedastisitas

d.     Multikolinearitas

e.      Autokorelasi (Khusus data time series)

Analisis regresi linear berganda sebenarnya sama dengan analisis regresi linear sederhana, hanya variabel bebasnya lebih dari satu buah. Persamaan umumnya adalah:

Y = a + b₁ X₁ + b₂ X₂ + .... + b_n X_n.

Y adalah variabel bebas,

X adalah variabel-variabel bebas

a adalah konstanta (intersept) dan

b adalah koefisien regresi pada masing-masing variabel bebas.

Langkah-langkah yang biasanya dipergunakan dalam analisis Regresi Linear Berganda adalah: 

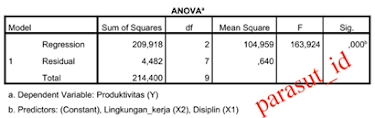
1)      Uji F

Bertujuan untuk mengetahui ada atau tidaknya pengaruh simultan /Bersama-sama/serentak yang diberikan semua variable X terhadap variable Y.

Analisis regresi linear berganda memerlukan pengujian secara serempak dengan menggunakan F hitung. Signifikansi ditentukan dengan membandingkan F hitung dengan F tabel atau melihat signifikansi pada output SPSS. Dalam beberapa kasus dapat terjadi bahwa secara simultan (serempak) beberapa variabel mempunyai pengaruh yang signifikan, tetapi secara parsial tidak. Sebagai ilustrasi: seorang penjahat takut terhadap polisi yang membawa pistol (diasumsikan polisis dan pistol secara serempak membuat takut penjahat). Akan tetapi secara parsial, pistol tidak membuat takut seorang penjahat. Contoh lain: air panas, kopi dan gula menimbulkan kenikmatan, tetapi secara parsial, kopi saja belum tentu menimbulkan kenikmatan.

   2)      Uji t.

Bertujuan untuk mengetahui ada atau tidaknya pengaruh parsial (sendiri) yang diberikan variable x terhadap variable y.

Nilai t hitung > t tabel berarti ada pengaruh yang signifikan antara variabel bebas terhadap variabel terikat, atau bisa juga dengan signifikansi di bawah 0,05 untuk penelitian sosial, dan untuk penelitian bursa kadang-kadang digunakan toleransi sampai dengan 0,10.

3)   Koefisien Determinasi  (R²)

Bertujuan untuk mengetahui berapa persen pengaruh yang diberikan variable x secara simultan terhadap y.

Koefisien Determinasi mencerminkan seberapa besar kemampuan variabel bebas dalam menjelaskan varians variabel terikatnya. Mempunyai nilai antara 0 – 1 di mana nilai yang mendekati 1 berarti semakin tinggi kemampuan variabel bebas dalam menjelaskan varians variabel terikatnya.

 Contoh Analisis Regresi Berganda

Judul : Pengaruh disiplin (X1) dan lingkungan kerja (X2) terhadap produktivitas kerja (Y)

Langkah penghitungan analisis regresi dengan menggunakan program SPSS

1.      Buka SPSS, klik Variable View. Pada bagian Name tulis X1, X2 dan Y. Pada Decimal ubah menjadi 0. Pada bagian Label tulis Disiplin, Lingkungan_kerja, dan Produktivitas. Pada bagian Measure pilih scale. Akan terlihat seperti ini:

2. Kemudian klik Data View. Masukan data total X1, X2 dan Y. Hasilnya seperti ini:

 3. Selanjutnya Analyse --> regression --> linear. Seperti gambar dibawah ini:

 

 4.       Pada jendela yang ada, klik variabel Y (Produktivitas) lalu klik tanda panah pada kotak dependent. Maka variabel tersebut akan masuk ke kotak sebagai variabel dependen. Lakukan dengan cara yang sama untuk variabel X1 dan X2 (independent).

 

5.      Lalu klik OK dan akan muncul output SPSS.

6.      Table output SPSS regresi linier berganda

Tabel Model Summary berisi tentang nilai koefisien determinasi (R square) yaitu kontribusi atau besar sumbangan pengaruh variable disiplin (X1) dan Lingkungan (X2) terhadap produktivitas (Y).

 Tabel Anova berisi informasi tentang ada tidaknya pengaruh X1 dan X2 secara simultan terhadap Y.

 Tabel Coefficients memberikan informasi tentang persamaan regresi dan ada tidaknya pengaruh variable X1 dan X2 secara parsial (sendiri-sendiri) terhadap variable Y.

 Rumus Persamaan Regresi linier berganda dalam penelitian ini  adalah:

Y = a + b₁ X₁ + b₂ X₂  atau

Y = 1.378 + 0,375 + 0,598 

Maknanya adalah jika disiplin (X1) naik 1 satuan maka nilai produkitvitas akan naik sebesar 0,375 dengan asumsi variable lain konstan. Jika nilai lingkungan kerja naik 1 satuan maka nilai produktivitas akan naik 0,598.

Untuk mengetahui cara melakukan uji F dan uji t dan mengetahui koefisien determinasi akan dibahas dalam topik lain. Silahkan Baca: 

Cara Uji F (Simultan) Regresi Linier Berganda

Tutorial Praktis Melakukan Uji t Analisis Regresi Linier Berganda

Cara Mudah Mengetahui Nilai Koefisien Determinasi (R²)